Unit 2 functions as the cornerstones of algebra answers, providing the foundation for understanding algebraic operations and equations. Functions represent relationships between variables, enabling the modeling of real-world phenomena. Common functions used in algebra include linear, quadratic, and exponential functions.
This unit explores the key properties of functions, including domain, range, and inverse functions, as well as the different types of function operations, such as composition, inverse, and transformation. Graphing functions is crucial for visualizing their behavior and understanding their properties.
1. Functions as the Building Blocks of Algebra
Functions play a fundamental role in algebra, serving as the basis for understanding algebraic operations and equations. They represent relationships between variables, enabling the modeling of real-world phenomena.
Common functions used in algebra include linear functions (y = mx + b), quadratic functions (y = ax^2 + bx + c), and exponential functions (y = a^x).
Properties and Operations of Functions
Functions possess key properties, such as domain, range, and inverse functions. Function operations include composition, inverse, and transformation, which are used to solve algebraic problems and analyze function behavior.
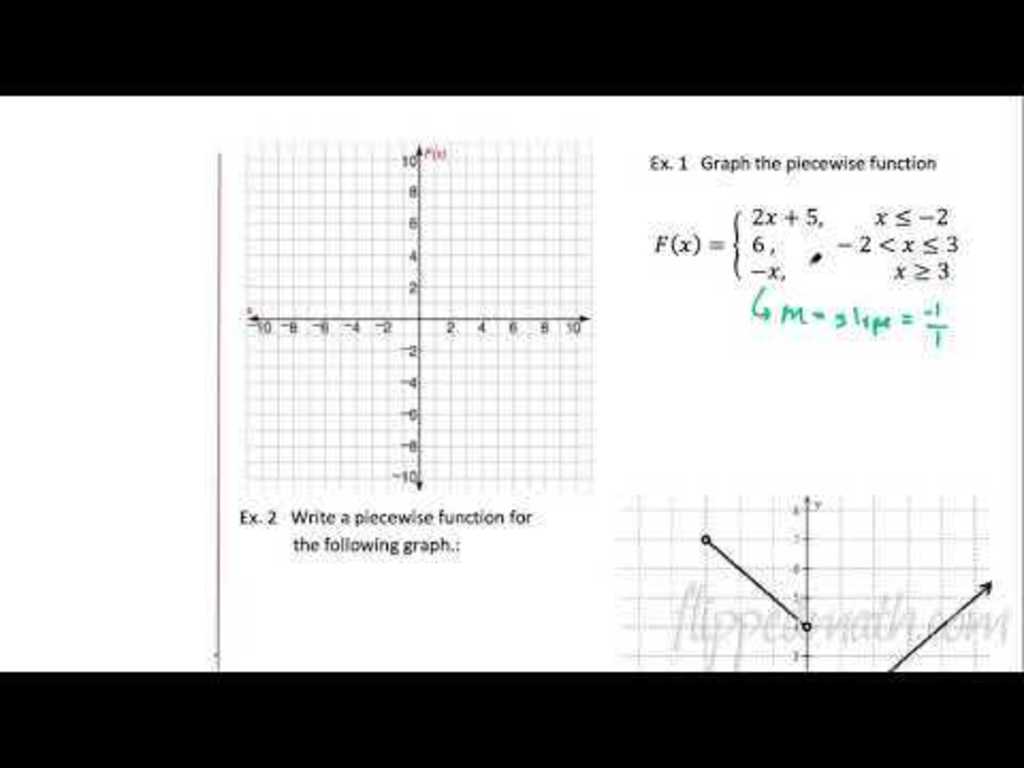
Graphing Functions, Unit 2 functions as the cornerstones of algebra answers
Graphing functions is crucial for visualizing their behavior and understanding their properties. Methods of graphing include point-plotting, transformations, and using technology. Graphing functions helps analyze function characteristics, such as intercepts, asymptotes, and extrema.
Applications of Functions in Real-World Problems
Functions are widely used to model and solve problems in various fields, including physics, engineering, and economics. They enable the modeling of population growth, projectile motion, and financial trends, helping us understand and predict real-world phenomena.
FAQ: Unit 2 Functions As The Cornerstones Of Algebra Answers
What are the key properties of functions?
Domain, range, and inverse functions.
What are the different types of function operations?
Composition, inverse, and transformation.
Why is graphing functions important?
To visualize their behavior and understand their properties.