Unit 3 Parent Functions and Transformations Homework 1 embarks on an enlightening journey into the realm of mathematical functions. This comprehensive guide unveils the intricacies of parent functions, their transformations, and their practical applications. Prepare to delve into a captivating exploration of function analysis, problem-solving techniques, and the art of applying mathematical principles to real-world scenarios.

Throughout this guide, we will unravel the fundamental concepts of parent functions, empowering you with the knowledge to identify and manipulate these foundational building blocks. We will explore the various transformations that can be applied to parent functions, equipping you with the skills to analyze and interpret function graphs.

Moreover, we will provide step-by-step guidance on applying transformations to functions, enabling you to confidently solve complex mathematical problems.

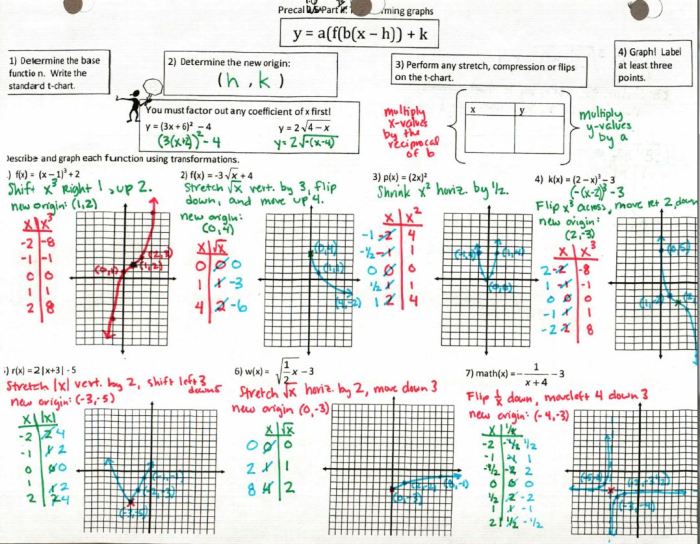
Parent Functions and Transformations

In mathematics, a parent function is a basic function that can be transformed to create a variety of other functions. Transformations are operations that change the shape or position of a function without changing its fundamental properties. Common parent functions include linear functions, quadratic functions, and exponential functions.

Analyzing Transformations, Unit 3 parent functions and transformations homework 1

To analyze transformations, we use function notation. Function notation allows us to represent transformations as operations applied to the parent function. For example, the notation f(x) + 2represents the translation of the function f(x)by 2 units up.

Applying Transformations

To apply transformations, we follow a series of steps. First, we identify the type of transformation (e.g., translation, reflection, dilation). Then, we determine the specific parameters of the transformation (e.g., the amount of translation or the scale factor for dilation).

Finally, we apply the transformation to the parent function using function notation.

Homework 1

Homework 1 for Unit 3 focuses on applying transformations to parent functions. Students will be asked to:

• Identify the type of transformation applied to a given function.
• Determine the parameters of the transformation.
• Apply the transformation to the parent function using function notation.

Students should review the concepts of parent functions and transformations before attempting Homework 1. They should also practice applying transformations to different types of parent functions.

Common Queries: Unit 3 Parent Functions And Transformations Homework 1

What are parent functions?

Parent functions are basic functions from which other functions can be derived through transformations.

What are the common types of transformations?

Common types of transformations include translations, reflections, and dilations.

How do I determine the equation of a transformed function?

To determine the equation of a transformed function, apply the transformation rules to the equation of the parent function.